제 2 장 프로세서
1. 자료의 표현 방법
1) 비수치적 데이터 표시법(Code)
< 컴퓨터 기본 코드 >
종 류 | 구성 bit 수 | 특 징 |
BCD 코드 | 6bit (2의6승) | 기본코드, 대․소문자 구별 못함.숫자는 4bit |
ASCII 코드 | 7bit (2의7승) | 통신용, 개인용 컴퓨터에서 많이 사용. |
EBCDIC 코드 | 8bit (2의8승) | 범용, 대․소문자 구별, 16진수 표현. |
① 8421 코드 : 10진수 1자리의 수를 2진수 4자리로 표현한 코드. (대표적인 가중치 코드)
가중치: 각 자라의 비트가 일정한 값(자기자리수)을 갖음 (8421,2421...)
비가중치 코드(각자리의 비트가 일정한 값을 갖지않는코드): 3초과 코드, 그레이 코드
② 3초과(excess-3)코드 : 8421 코드에 3(0011)을 더해서 만든 코드.
(비가중치 코드, 자기보수 코드)
10진수 | 3초과 코드 | 10진수 | 3초과 코드 |
0 1 2 3 4 | 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 | 5 6 7 8 9 | 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 |
0+3=-3 0011(8421코드)
③ 2421 코드 : 각 자리마다 가중치가 1, 2, 4, 2 순으로 주어지는 코드.
(가중치 코드, 자기보수 코드)
④☆그레이(gray)코드 : 비가중치 코드로 연산이 불가능하며, 입출력 장치,
A/D 변환기(디지털 아날로그변환) 등으로 사용. (오류적음)
gray → 2진수 | 2진수 → gray |
1 1 1 0(gray) ↓↗↓↗↓↗↓ 1 0 1 1(2진수) | 1 → 0 → 1 → 1(2진수) ↓ ↓ ↓ ↓ 1 1 1 0(gray) |
(최상위 비트는 그대로, 1+1=2 => 0 옆의 값과 더해 합만 적고 나머지버려, 0+1=1)
⑤ 패리티 비트(Parity bit) : 에러 검출 코드
㉠ 홀수 패리티(add parity) : 비트 내의 '1'의 수가 홀수( )
)
㉡ 짝수 패리티(even parity) : 비트 내의 '1'의 수가 짝수(p=x⊕y⊕z)
< 3비트 패리티 비트 >
x y z | 홀수 P | 짝수 P |
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 | 1 0 0 1 0 1 1 0 | 0 1 1 0 1 0 0 1 |
(짝-->홀p=1 홀-->짝p=1)
※패리티 비트의 장점과 단점
장 점 | 한 비트만으로 에러를 검출할 수 있다. |
단 점 | 에러를 교정할 수 없으며, 두 비트 이상 에러 발생시 검출 못함. |
⑥ 해밍 코드(Hamming Code) : 해밍코드는 착오를 검출하고 교정할 수 있다.
㉠ 패리티 비트의 위치 : 1, 2, 4, 8, 16, 32… ( 1, 2의 배수....)
㉡ 기본 해밍 코드 : 패리티 비트 3개와 8421 코드로 구성. (P1 P2 8 P3 4 2 1)
2) 수치적 데이터 표현
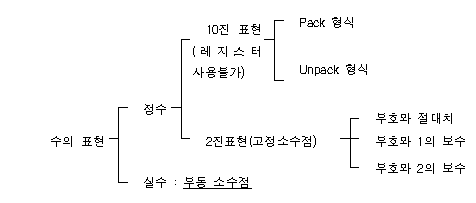
① 고정 소수점 수(Fixed Point Number)
종 류 | 표현 범위 | 특 징 |
부호와 절대치 | -(2n-1-1) ~ 2n-1 | ․양수인 경우 3가지 표현 동일.(보수는 음수일때만 생성=>양수일 때는 값같다. ) ․3가지 중 부호와 2' (=2의보수)표현이 제일 범위가 넓다. ․부호와 2'는-0이 없다.(여기만-0값없다) |
부호와 1의 보수 | -(2n-1-1) ~ 2n-1 | |
☆부호와 2의보수 | -2n-1~2n-1-1 |
② 10진 표현
종 류 | 특 징 | -123 표현 |
Pack 형식 | 한 수 표현시 4bit, 부호비트는 마지막 추가되는 4bit. (+:1100=12 16진수C+, -:1101=13 => D-) | 0001 0010 0011 1101 1 2 3 D |
Unpack 형식 | 한 수 표현시 8bit(EBCDIC 형식), 부호 비트는 마지막 숫자의 존. (+:1100=C12, -:1101=D13) | 11110001 11110010 11010011 F 1 F 2 D 3 |
EBCDIC 형식에서 4BIT는 F로 표현
③ 부동소수점 (Floating Point Number)
㉠ 부호, 지수, 소수(가수)로 구성.
㉡ 소수점 위치 : 부호와 지수 사이.
㉢ 정규화 하는 이유 : 보다 큰 수 표현을 위해.(표현 범위 넓게)
2. 명령어 형식과 주소지정
1) 연산자(operation code) : 수행해야할 범위명시
― 명령어는 크게 연산자(op-code: 동작부분), 자료(operand : 주소부분)로 구성.
op-code | operand | ||
Mode | Register | Address | |
․동작 코드(operation code) : 수행해야 할 동작 명시.
․모드(mode) : 1비트(간접 주소 : 1, 직접 주소 : 0)
※동작 코드가 n bit → 명령어 개수는 2n.
※주소 비트가 n bit → system 용량은 2n.
2) ☆연산자 기능
① 함수연산 기능 (논리연산과 산술연산)② 제어기능(통제.지시.감독) sma,Jump명령
③ 입출력 기능 ④ 전달 기능(load: memory주기억→cpu중앙처리, store저장 : cpu → memory)
3) 주소 지정 방법(명령어 형식)
① 0 주소 지정 : Stack (가장 빠르다.)
연산자 |
② 1 주소 지정 : 누산기(Accumulator)
연산자 | 주소 |
③ 2 주소 지정 : 범용, 입력자료상실(주소1+주소2=>주소1)
연산자 | 결과(주소1) | 주소2 |
④ 3 주소 지정 : 범용,가장느림, 연산후입력자료 보존(주소1+주소2=주소3), 프로그램 길이단축
연산자 | 결과(주소1) | 주소2 | 주소3 |
4) 주소 지정 종류
① Implied Addressing Mode(묵시적 주소 지정)
② Immediate Addressing Mode(즉시 주소 지정) : operand 값이 실제 자료(메모리 참조=0번)
③ Direct Addressing Mode(직접 번지 지정) : operand 값은 실제자료의 주소(메모리 참조 = 1번)
④ Indirect Addressing Mode(간접 번지 지정) : 메모리 참조 = 2회 이상
⑤☆Relative Addressing Mode(상대 번지 지정) : 계산에 의해 실제 자료의 주소 산출. (operand + 프로그램 카운터)
ex) LDA(연산자) 120(주소값),PC(프로그램 카운터)= 100
주소 | 내용 | |
⋮ | ⋮ | |
120 | 200 | |
⋮ | ⋮ | 즉시 주소 : 120 |
200 | 220 | 직접 주소 : 200 |
⋮ | ⋮ | 간접 주소 : 220 |
220 | 300 | 상대 주소 : 300 |
120(=>200)+ 100 =300
3. 중앙처리 장치
1) 프로세서 수행 과정
명령어 인출 → 명령어 해석 → 데이터 인출 → 데이터 처리 → 데이터 쓰기
2) 레지스터(register)
― 컴퓨터의 중앙처리 장치에서 사용되는 고속 메모리로서,
처리에 필요한 내용을 일시적으로 기억. (새로운 값 들어오면 소멸)
① Accumulator(누산기) : 연산시 피가수 및 연산결과를 일시적으로 기억하는 레지스터.
② 프로그램 카운터(PC) : 다음에 실행할 명령어의 번지 기억.
③ 명령 레지스터(IR) : 현재 수행 중인 명령의 내용 기억.
④ 기억장치 주소 레지스터(MAR) : 메모리의 번지를 해독.
⑤ 기억장치 버퍼 레지스터(MBR) : 기억장치에 출입하는 자료를 기억.
3) 중앙 처리 장치 4대 기능
기억기능, 연산기능, 전달기능, 제어기능
4. 연산장치(ALU : Arithmetic Logic Unit): 산술연산과 논리연산수행
1) 연산의 종류
① 자료의 성질에 따른 분류
㉠ 비수치적 연산(논리연산) : 논리 shift, rotate, move, AND, OR, complement 등
㉡ 수치적 연산(산술연산): 고정 소수점 연산, 부동 소수점 연산, Pack 연산, 산술 shift 등
② ☆★자료의 수에 따른 분류
㉠ 단항(unary) : shift, rotate, complement 등
㉡ 이항(binary) : AND, OR, 사칙연산 등
2) 비수치적 연산
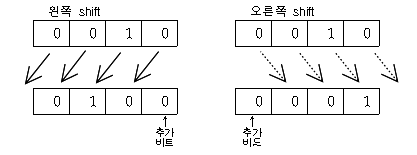
Shift (자리이동) : 모든 비트들을 서로 이웃한 비트의 자리로 옮기는 것.(추가비트는 0이됨)
3) 수치적 연산
① 연산시 1의 보수법을 이용한 경우는 캐리(올림수)가 발생하면, 캐리를 다시 더하고,
2의 보수법을 이용한 경우는 무시.
② overflow : 연산 후 결과값이 수의 표현 범위를 벗어나는 경우.
(두 수가 양수이거나 음수인 경우 발생)
③ 산술적 shift :왼쪽 shift이용→ 곱셈(2로 곱하는), 오른쪽 shift이용 → 나눗셈(2로 나누는)
기존의 부호비트는 그대로 있다. ※ 왼쪽 산술 shift(곱셈)
종류 | Padding 비트 | overflow |
부호와 절대치 | padding 비트 : 항상 0 | 잃어버린 비트 = 1 |
부호와 1' | padding 비트 : 양수→0, 음수→1 | 잃어버린 비트 ≠ 부호 비트 |
부호와 2' | padding 비트 : 항상 0 | 잃어버린 비트 ≠ 부호 비트 |
※ 오른쪽 산술 shift(나눗셈)
종류 | Padding 비트 | truncation |
부호와 절대치 | padding 비트 : 항상 0 | 잃어버린 비트 = 1 |
부호와 1' | padding 비트 : 양수→0, 음수→1 | 잃어버린 비트 ≠ 부호 비트 |
부호와 2' | padding 비트 : 양수→0, 음수→1 | 잃어버린 비트 = 1 |
4) 부동 소수점 연산
① 덧셈, 뺄셈
0인지 여부 조사 → 가수 위치 조정(소수점 통일) → 가수에 대한 덧셈 및 뺄셈 → 정규화(분해하는 과정) |
② 곱셈
0인지 여부 조사 → 지수 덧셈 → 가수 곱셈 → 정규화 |
③ 나눗셈
0인지 여부 조사 → 부호 결정 → 피젯수 위치 조정 → 지수 뺄셈 → 가수 나눗셈 |